|
|
Геометрия плиток.16.10.2008 |
|
Магия шестиугольника.Из-за того, что использование пятиугольников и многоугольников с семью и более сторонами в правильных плиточных моделях невозможно, главными числами в таких моделях являются 2, 3, 4 и 6. Особое значение для пифагорейцев представляло число 6. Это треугольное число: 6=1+2+3. Оно также «совершенное» число – без остатка делится на (меньшие) числа 1, 2 и 3; в сумме они равны 6, числу, с которого мы начали. Следующее совершенное число – 28 с делителями 1, 2, 4, 7, 14, составляющими в сумме 28. Это тоже треугольное число, равное 1+2+3+4+5+6+7.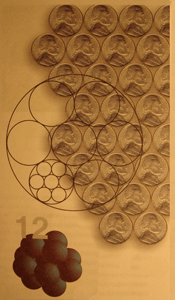
Сегодня ничего из этой «науки» о магических числах не считается важным для математики. Теперь это не болле чем незначительный исторический курьез. Однако число 6 действительно имеет важное значение для математики – это «целующее число» в двухмерном пространстве. То есть если вы нарисуете на плоскости окружность и постараетесь расположить несколько других окружностей того же размера так, чтобы каждая касалась («целовала») первую, но ни одна не накладывалась бы на другую, то вокруг первой вы разместите точно шесть окружностей. В результате получится сотовая модель.В трех измерениях, где окружности заменяются шарами, «целующим числом» будет 12. Правда, в трех измерениях подгонка уже не будет точной: между двенадцатью шарами имеются пустоты, оставляющие место для вращения. Математикам известно «целующее число» только для двух других пространственных измерений: 8 и 24. Более разумные измерения вроде 4 или 5 остаются загадкой, но в обоих случаях есть полный ответ…полное безумие. Кажется, дело в каких-то довольно причудливых совпадениях; однако, без тени сомнения можно сказать, что в восьми измерениях «целующее число» равно 240, а в 24 измерениях – 196560. Симметрия и искусство.
У исламских художников долгое время существовала традиция использования абстрактных композиций, особенно при украшении мечетей и других важных сооружений. Они вообще чувствовали тесную связь между геометрией рисунков и геометрией Вселенной и использовали математические модели для прославления Создателя.Математика симметрии проникла в западное искусство несколько иным путем, в эпохе Возрождения, когда художники и математики объединили усилия, разрабатывая теорию перспективы. Теория перспективы включает математику симметрии, потому что соотносит строгие законы движения в трехмерном пространстве с неизбежными искажениями на двухмерной проекции на холст художника. Одним из художников, который намеренно прибегал к симметрическим моделям, был Мориц Эшер. Взгляните на его композицию «Ангелы и дьяволы». Пять симметрий запрещены.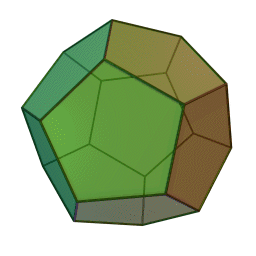
Ни одна кристаллическая решетка не может обладать пятью вращательными симметриями. Их может быть 2, 3, 4 или 6.«Порядок» вращательной симметрии означает, сколько раз ее надо выполнить, чтобы вернуться туда, откуда начали. Порядок 2 – это вращение на 180 градусов, порядок 3 – на 120 градусов, порядок 4 – на 90 градусов, порядок 6 – на 60 градусов.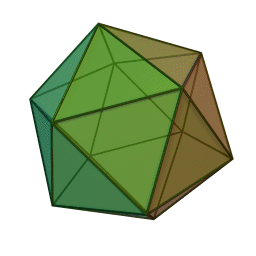 
Кристаллы могут иметь форму куба (поваренная соль), октаэдра и тетраэдра. Однако ни один кристалл не может принять форму додекаэдра или икосаэдра,
потому что кристаллографическая ограниченность исключает пять симметрий.
Или, может быть, нет.
В коллекции плиточных моделей оксфордского физика Роджера Пенроуза законы кристаллографии смягчены до предела, поскольку сами модели строятся на пятиугольниках. Поначалу они были забавными игрушками и увлекательным материалом для чистых математиков, но практическое их применение равнялось нулю. Все изменилось в 1984 году, когда оказалось, что природа прекрасно использует узоры, подобные придуманным Пенроузом, правда, в трехмерном пространстве.
Пенроуз придумал две плиточные формы, названные змеей и дротиком и полученные разрезанием пятиугольника на простые части. Змея представляет одну пятую пятиугольника, а дротик – это то, что нужно добавить к змее, чтобы получить ромб. Из комплекта змей и дротиков можно собрать на плоскости бесконечное множество самых разных фигур. Одна из них – Солнечный узор, обладает идеальной пятикратной симметрией: в центре находятся пять змей, воссоздающих исходный пятиугольник. Есть еще Звездный узор – с пятью дротиками в центре.
Однако законы кристаллографии не нарушаются, потому что модели Пенроуза не являются решетками. Однако они к ним намного ближе, чем ожидалось до удивительного открытия Пенроуза. Модели Пенроуза не периодичны, но квазипериодичны. Это означает, что любая их ограниченная часть повторяется до бесконечности, но не всегда с идеальной регулярностью.В 1984 году Даниэль Шехтман обнаружил первый квазикристалл – сплав алюминия с марганцем, атомы которого располагались в квазирешетчатых структурах. 
Это был новый вид существования. Скоро появились и другие примеры, скажем, сплав алюминия, лития и меди с шестью атомами алюминия и тремя лития на атом меди.Мораль сей истории такова: математические модели имеют ограничения. Допустимое поведение зависит от ограничений, установленных для модели. Природа имеет дело с реальными вещами, а не с моделями, и не всегда подчиняется ограничениям, которые находят удобными для себя математики. Источник: "Какой формы снежинка? Магические цифры в природе", И. Стюарт. |
 
|
|
|
Плиточный пол – одна из великих констант человеческой культуры. Правильными узорами укладывали каменные плиты египтяне; правильными узорами выкладывали свои мозаики древние греки и римляне. Самой простой плиточной моделью представляются выложенные в виде шахматной доски одинаковые квадратные плитки. Кроме квадратов в большинстве правильных моделей используются правильные многоугольники – формы с равными сторонами и равными углами.
Какими многоугольниками можно выложить плоскую поверхность, если применять лишь одну форму плиток? Ответ простой: равносторонние треугольники, квадраты, шестиугольники и больше ничего.